js实现二叉树之顺序存储

假设现在我们已经把数据存到数组中：[1, 3, 4, 6, 8, 10, 2, 5]，其存储可表示如下：

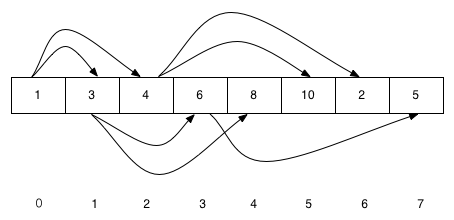
对于任意节点，我们怎么找到它的父节点和左右子节点？

1
2
3
4
5
索引为0的节点，没有父节点，左子节点索引为1，右子节点索引为2；
索引为1的节点，父节点索引为0，左子结点索引为3，右子节点索引为4；
索引为2的节点，父节点索引为0，左子结点索引为5，右子节点为索引为6；
...
索引为i的节点，父节点索引为Math.floor((i - 1) / 2)，左子结点索引为2i + 1，右字节点为索引为2i + 2

将数组表示二叉树的形式，应该长这样（最左边数字表示树的层序号）：

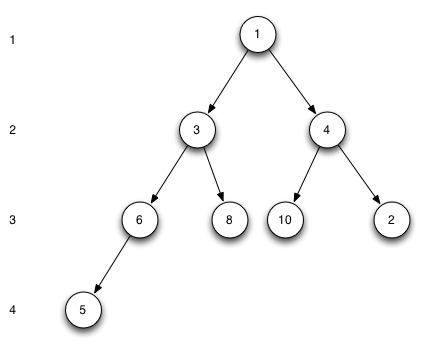
表示成二叉树结构之后，我们该怎么索引节点？ 一般会用到以下两个参数：

  • level，节点所在的层，从1开始
  • order，节点在当前层中的序号（从左至右），从1开始

例如上图，节点3可以通过level = 2, order = 1来定位，再如节点8，可以通过level = 3, order = 2来定位。

观察一下，我们可以发现以下规律（从根节点开始顺序左往右数）：

1
2
3
4
5
6
7
第一层第一个节点序号：1
第二层第一个节点序号：2
第三层第一个节点序号：4
第四层第一个节点序号：8
...

第k层第一个节点：Math.pow(2, k - 1)

有了以上规律，我们现在就可以来映射一下level、order与数组下标之间的关系：

1
2
3
4
5
// storage mapping function
// level、order从1开始
function smf(level, order) {
    return Math.pow(2, level - 1) + order - 2;
}

为啥-2？因为数组的索引是从0开始的，而我定义的level、order都是从1开始的（其实你也可以让它们从0开始）。

通过以上函数获取索引之后，就可以直接从数组中取出节点。

基本操作

先定义一个构造器，表示二叉树类：

1
2
3
4
5
function SqBinaryTree(data) {
    data = data || [];
    // 顺序存储空间
    this.nodes = data.slice(0);
}

data参数表示用户输入的数据，二叉树构造器要做的就是把数据存储到nodes中，然后我们就可以用树的形式来访问数据。

现在我们就可以通过以下方式来获得一颗顺序存储二叉树：

1
var sbt = new SqBinaryTree([1, 3, 4, 6, 8, 10, 2, 5]);

获取深度

一棵树的深度就是它的层数，怎么计算呢？

顺序存储可能不是紧凑的，比如：[1, undefined, 3, 2, 10, 12]，其中的undefined表示该位置没有节点。

因此要计算深度得先从后往前找到最后一个非undefined的节点，该节点所在的索引+1就是总的节点数，然后就可以用一个循环来计算深度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
SqBinaryTree.prototype.getDepth = function() {
    var n = this.nodes.length;
    // 找到最后一个节点
    while(--n) {
        if (this.nodes[n] !== undefined) {
            break;
        }
    }
    // 总节点数
    n += 1;

    var k = -1;

    // 深度为k的二叉树最多有2^k - 1个节点
    do {
        k++;
    } while (Math.pow(2, k) - 1 < n);

    return k;
}

例如:

1
sbt.getDepth(); // 4

获取节点

获取指定位置的节点：

1
2
3
4
5
SqBinaryTree.prototype.getNode = function(level, order) {
    var idx = smf(level, order);

    return this.nodes[idx];
}

插入节点

在指定位置上插入节点时，如果待插入节点的位置上没有对应的父节点，则无法插入，如下图所示：

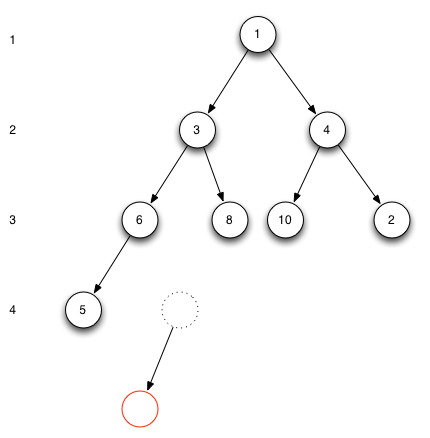
红色圆框表示待插入节点的位置，虚线框表示该位置上没有节点，此时如果在红色圆框位置插入节点，因为红色圆框的父节点虚线框的位置上不存在节点，因此插入失败：

1
2
3
4
5
6
7
8
9
SqBinaryTree.prototype.setNode = function(level, order, value) {
    var idx = smf(level, order);
    if (this.nodes[Math.floor((idx - 1) / 2)] === undefined) {
        return false;
    }

    this.nodes[idx] = value;
    return idx;
}

删除节点

本文实现的二叉树是一个普通的二叉树，没有特殊二叉排序树那种约束，因此删除节点时就不需要重建树了，直接把待删除节点的整颗子树都删掉即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
SqBinaryTree.prototype.deleteNode = function(level, order) {
    var idx = smf(level, order);
    if (this.nodes[idx] === undefined) {
        return false;
    }
    var queue = [idx];
    var k = queue.shift();
    while(k !== undefined) {
        if (this.nodes[2 * idx + 1] !== undefined) {
            queue.push(2 * idx + 1);
        }
        if(this.nodes[2 * idx + 2] !== undefined) {
            queue.push(2 * idx + 2);
        }
        // 删除节点
        this.nodes[idx] = undefined;

        k = queue.shift();
        idx = k;
    }

    return true;
}

源代码已经放在Github上了，有兴趣的可以围观一下，传送门。

参考文章